4) 2. Théorie des poutres
Définitions et hypothèses Poutre : Une poutre est un corps dont une dimension est très grande par rapport aux deux autres : F (section droite...
Définitions et hypothèses
- Poutre : Une poutre est un corps dont une dimension est très grande par rapport aux deux autres : F (section droite ) << L (longueur)
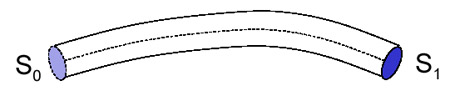
Une structure simple peut-être assimilée à une poutre.
Poutre : schématisation
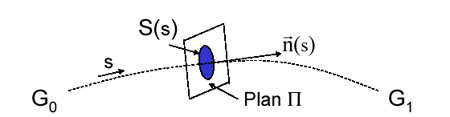
Notations :
- s: abscisse curviligne
- G0G1: ligne moyenne (fibre moyenne)
- P: plan de la section droite S(s)
- S(s): section droite (plane, perpendiculaire à la ligne moyenne)
- G(s):centre d'inertie de S(s)
- N(s): normale à la section droite
- Si la fibre moyenne est plane, la poutre est dite plane (G0G1 Є plan)
- Si la fibre moyenne est rectiligne, la poutre est dite droite (G0G1 = droite)
- Si la fibre moyenne est plane et que la section droite admet ce plan comme plan de symétrie, la poutre est dite à plan moyen.
- s: abscisse curviligne
- G0G1: ligne moyenne (fibre moyenne)
- P: plan de la section droite S(s)
- S(s): section droite (plane, perpendiculaire à la ligne moyenne)
- G(s):centre d'inertie de S(s)
- N(s): normale à la section droite
- Si la fibre moyenne est plane, la poutre est dite plane (G0G1 Є plan)
- Si la fibre moyenne est rectiligne, la poutre est dite droite (G0G1 = droite)
- Si la fibre moyenne est plane et que la section droite admet ce plan comme plan de symétrie, la poutre est dite à plan moyen.
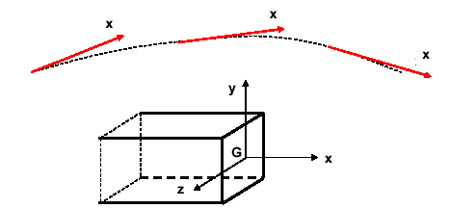
Convention :
Le système d'axes utilisé pour une section droite est
centré en G et tel que Gx est tangent à la fibre
moyenne. Gy est pris vertical vers le haut. Gz est
définit pour compléter le système orthonormé Gxyz.
Matériau :
- homogène
- isotrope
- comportement élastique linéaire -* les déformations et les déplacements sont supposés petits -* les équations étant linéaires, les états de déformations et de contraintes peuvent être superposés -* Les équations d'équilibre sont formulées pour la structure avant la déformation.
- homogène
- isotrope
- comportement élastique linéaire -* les déformations et les déplacements sont supposés petits -* les équations étant linéaires, les états de déformations et de contraintes peuvent être superposés -* Les équations d'équilibre sont formulées pour la structure avant la déformation.

Articles en rapport
-
La théorie de l'autonomie de la volonté en matière contractuelle
La théorie de l'autonomie de la volonté représente le fondement de la force obligatoire du contrat dans la mesure où, à...
-
2.3 Remarques Théorie des poutres
RemarquesLes résultats que nous obtiendrons par la théorie despoutres sont d'autant plus exacts que : Le rayon de courbure de...
-

2.7 Equilibre des poutres
-
Formulaire : flèches de poutres isostatiques
Voici un formulaire sur les flèches de poutres isostatiques:


