Produit scalaire
Soit le plan E Soient deux vecteurs $vec u $et$vec v$de E, et trois points O, A et B tels que :$vec u $=$vec OA$ et $vec v$=$vec OB$ On...
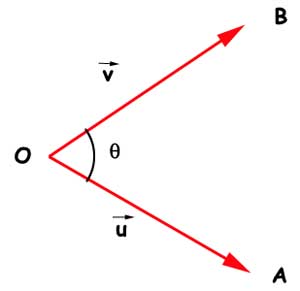
Plan E
-On appelle produit scalaire de deux vecteurs $vec u $et$vec v$le nombre réel noté $vec u $.$vec v$tel
que$vec u $.$vec v$=$|vec u|$x$|vec v|$x$costheta$
_ Donc $vec u $.$vec v$= OAxOBxcos$theta$
Propriétés
-Si les vecteurs $vec u $.$vec v$ sont colinéaires et de même sens :
_ $theta$=0 -> cos$theta$=1 -> $vec u $.$vec v$=$|vec u|$x$|vec v|$
-Si les vecteurs $vec u $.$vec v$ sont colinéaires et de sens contraires :
_ $theta$=$pi$ -> cos$theta$=-1 -> $vec u $.$vec v$=-$|vec u|$x$|vec v|$
Quels que soient les vecteurs $vec u $,$vec v$ et $vec w$ de E et deux réels α et β :
-(α$vec u$)⋅(β$vec v$) = (αβ)×($vec u$ ⋅$vec v$)
-$vec w$⋅($vec u$+$vec v$)= $vec w$ ⋅$vec u$ +$vec w$ ⋅$vec v$
-($vec u$+$vec v$)$^2$=$|vec u|^2$+$|vec v|^2$+2$vec u$.$vec v$
-($vec u$-$vec v$)$^2$=$|vec u|^2$+$|vec v|^2$-2$vec u$.$vec v$
-($vec u$+$vec v$).($vec u$-$vec v$)=$|vec u|^2$-$|vec v|^2$
-Si $vec u$⊥$vec v$ alors $vec u $.$vec v$=0

Articles en rapport
-
Produit de matrices en notation indiciel
Soient 2 matrices $A$ et $B$ de dimension (n,n). Leur produit $P$ est de même dimension et défini par : $$begindisplaymath...


