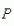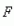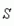Cours de MMC Page 1 (mécanique des milieux continus)

$Au\; sens\; strict\; du\; terme,\; la\; mécanique\; des\; milieux\; continus\; (abrégée\; "M.M.C."\; parfois)\; est\; la\; branche\; de\; la\; mécanique\; qui\; se\; propose\; d\text{'}étudier\; l\text{'}étude\; des\; mouvements,\; des\; déformations,\; des\; champs\; de\; contraintes\; au\; sein\; de\; milieux\; continus.$Définition :
- D1. Nous désignons par "milieu" tout fluide (solide, liquide, gaz ou plasma selon ce que nous avons vu en thermodynamique), déformable ou non, quand nous le considérons d'un point de vue macroscopique, par opposition à une description corpusculaire.
- D2. Nous désignons par "milieur continu" un milieu tel que si M et M' appartiennent à un milieu et si M' appartient au voisinage M, alors quelle que soit la déformation subie par ce milieu, dM' appartiendra au voisinage de dM. Cette branche apparaît souvent comme la science de l'ingénieur qui permet de comprendre et de décrire le monde matériel qui nous entoure et les phénomènes courants qui s'y déroulent: mouvements de liquides, de gaz, vol des avions, hélicoptères, fusées, satellites, navigation des bateaux, déformations des corps solides, structure interne des étoiles, etc. Par ses attaches à la mécanique thermique (thermodynamique), elle s'étend jusqu'à la thermique, l'énergétique, l'acoustique. Prenant en compte les comportements des milieux continus, elle englobe l'hydrodynamique, la dynamique des gaz, l'élasticité, la plasticité et d'autres comportements. Elle est la clé de ce que nous appelons aujourd'hui la "modélisation", qui n'est autre que l'art d'analyser un phénomène physique et de le décrire en termes mathématiques, ce qui permet de l'étudier avec la rigueur propre à cette discipline. Cette section du site est séparée en 4 parties principales: solides, liquides, gaz et plasmas. Dans chaque partie, nous introduirons les outils mathématiques spécifiques à l'étude de tel ou tel milieu continu avec une complexité (toute relative) croissante. Cependant, par choix il a été décidé d'exposer les théorèmes avec les outils mathématiques les plus simples possibles mais tout en arrivant aux mêmes résultats. Ainsi, par exemple, l'équation de Navier-Stokes qui prendrait 150 pages de développements mathématiques rigoureux n'en prend plus que 27. Il y a donc un avantage non négligeable aussi bien pour l'auteur que pour le lecteur à procéder ainsi. Remarque : concernant les équations de Navier-Stokes, nous donnerons des exemples pratiques de celles-ci lors de notre étude de la météorologie.

Des atomes d'un même élément ou d'éléments différents s'assemblent en des édifices spécifiques. Cela conditionne la force de leurs interactions électriques, qui définissent la structure finale de la substance. Dans les conditions normales sur notre planète, la matière existe à l'état solide, liquide, gaz ou plasma. Si les forces interatomiques sont assez intenses , la collection de particules conserve sa forme et son volume. Cette propriété de conserver la forme et le volume, ainsi que des propriétés élastiques distinguent les solides.

Les notions de "compression" et "contrainte" (que nous pouvons englober dans le terme de "pression") sont de première importance en mécanique des fluides. Il convient donc de définir ces différents types de pression avec le plus de rigueur possible.
- D1. Nous appelons "pression de compression" et nous notons traditionnellement $P$ le rapport entre la force $F$ qui s'exerce (s'appuie) sur un élément de surface $S$. Ainsi, sous forme scalaire :

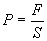
Si une force agit sur une surface finie, nous parlons alors de "force répartie".
- D2. Nous appelons "pression de contrainte" et nous notons le rapport entre la force $F$ qui tire sur un élément de surface $S$ . Ainsi, sous forme vectorielle :

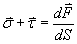
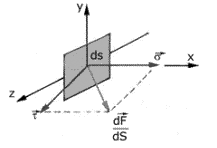
où $vec sigma$ et $ vec tau $sont respectivement les contraintes normales et tangentielles. Nous pourrions très bien englober les deux définitions ci-dessus en une seule et travailler avec les signes des forces. Mais par souci de cohérence avec ce qui est enseigné dans les écoles, nous garderons ces deux définitions qui s'identifient par définition par le fait que leurs forces sont opposées par rapport à un élément de surface $S$.